[Список тем]
Эквивалентность КА: теорема Мура
Две булевы функции Ф и F эквивалентны, если на всех возможных интерпретациях
они принимают одинаковые значения. Поскольку число интерпретаций у булевыx
функций конечно, то, перебрав их все, можно проверить, эквивалентны ли Ф и F.
Если число интерпретаций велико, можно привести Ф и F к нормальной формe и
сравнить их представления. Для проверки эквивалентности Ф и F можно также
проверить аналитически, будет ли общезначима функция Ф = F.
Иная ситуация с конечными автоматами. Два конечных автомата эквивалентны, если
реализуемые ими отображения вход-выход эквивалентны. Конечный автомат реализует
отображение бесконечного множества входных последовательностей сигналов в
бесконечное множество выходных последовательностей сигналов. Поэтому автоматные
отображения нельзя сравнить простым перечислением их значений на всех возможных
аргументах. Дадим несколько определений.
Расширим функции перехода и выхода автомата так, чтобы они были определены на
множествах последовательностей (цепочках) сигналов входного алфавита.
Пусть 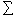 - алфавит (конечное множество
символов) и
- алфавит (конечное множество
символов) и 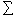 * множество
цепочек из элементов
* множество
цепочек из элементов 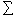 . Будем о
бозначать ε пустую цепочку, вовсе не содержащую символов, а ^ - операцию
конкатенации (склеивания) цепочек. Так, аав^ва = аавва. Знак операции
конкатенации часто опускают. Цепочки будем обозначать малыми греческими
буквами
. Будем о
бозначать ε пустую цепочку, вовсе не содержащую символов, а ^ - операцию
конкатенации (склеивания) цепочек. Так, аав^ва = аавва. Знак операции
конкатенации часто опускают. Цепочки будем обозначать малыми греческими
буквами
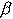 ,
,
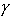 .
Очевидно, ε является как левой, так и правой единицей
для операции конкатенации:
аε = εа = а.
.
Очевидно, ε является как левой, так и правой единицей
для операции конкатенации:
аε = εа = а.
| Определение 3 |
Пусть А = <S, X, Y, s0, , ,
 > - конечный автомат. > - конечный автомат.
Расширенными функциями
перехода и выхода автомата А называются функции
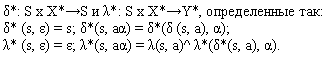
|
Расширенные функции переходов и выходов определены на множестве входных
последовательностей (входных цепочках) в отличие от обычных функций переходов
и выходов, которые определены на множестве входных сигналов.
Пусть в некоторое состояние автомата не существует пути из начального
состояния. Иными словами, в эти состояния автомат не может попасть.
Такие состояния автомата называются недостижимыми, остальные - достижимыми.
Очевидно, что недостижимые состояния и переходы из них можно отбросить:
они не влияют на поведение конечного автомата. Дадим формальное определение.
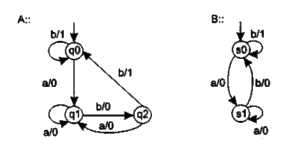
Рис. 5. Два конечных автомата
Достижимое множество состояний конечного автомата А = < S, X, Y,
s0, ,
,  >
строится с помощью алгоритма, основанного на индукции. Алгоритм разобьем на
последовательные шаги. На i-м шаге будем строить множество Qi состояний,
достижимых из начального состояния автомата некоторой входной цепочкой длины
не более чем i. Очевидно, что Q0 = {S0}.
Для любого i очевидно определение
>
строится с помощью алгоритма, основанного на индукции. Алгоритм разобьем на
последовательные шаги. На i-м шаге будем строить множество Qi состояний,
достижимых из начального состояния автомата некоторой входной цепочкой длины
не более чем i. Очевидно, что Q0 = {S0}.
Для любого i очевидно определение
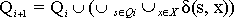 .
Очевидно также, что не более чем за |S| шагов
Qk+i = Qk.
Это множество состояний Qk будет включать в себя все
достижимые состояния автомата
А = <S, X, Y, s0,
.
Очевидно также, что не более чем за |S| шагов
Qk+i = Qk.
Это множество состояний Qk будет включать в себя все
достижимые состояния автомата
А = <S, X, Y, s0, ,
,
 >
Вернемся теперь к проблеме эквивалентности конечных автоматов.
>
Вернемся теперь к проблеме эквивалентности конечных автоматов.
| Определение 5 |
Конечные автоматы А = <SA, ХA, YA, S0A,  А, А,  .А> и В = <Sв, Хв, Yв, S0в, .А> и В = <Sв, Хв, Yв, S0в, , , > называются эквивалентными, если выполнены два условия: > называются эквивалентными, если выполнены два условия:
а) их входные алфавиты совпадают: ХА = Хв = X;
б) реализуемые ими отображения совпадают: ( 
 X *) X *)  А *
(SOA, а) = А *
(SOA, а) =  в *(S0B , а). в *(S0B , а).
|
Два конечных автомата (см. рис. 5) имеют разное число состояний
и эти состояния по-разному называются. Но внешнее поведение у них похожее:
реакция первого автомата на входную цепочку aabbabb равна
 A*(q0, aabbabb) =
A*(q0, aabbabb) =
 B*(SO, abbabb) = 0001001.
B*(SO, abbabb) = 0001001.
Однако ответить на вопрос, эквивалентны ли эти автоматы,
перебором их реакций ia всех входные цепочки невозможно:
входных цепочек бесконечно много.
Поэтомy проблема эквивалентности конечных автоматов является нетривиальной.
Оказывается, существует простой метод решения этой проблемы.
Этот метод основан на понятии прямого произведения конечных автоматов.
| Определение 6 |
Прямым произведением конечных автоматов
А = <SA, X, YA, S0A,
 A, A,
 A.А>
и В = <SB, X, YB, S0B, A.А>
и В = <SB, X, YB, S0B,
 B, B,  B> B>
с одинаковым входным алфавитом X (обозначается А х В)
называется автомат
А х В = <SAx SB, X, YA x
YB, (S0A,
S0B), A x B, A x B,
 А x В> ,
где: А x В> ,
где:
a) ( sA sA SA)
( SA)
( sB sB SB)
( SB)
( x x X) X)
 AxB((SA,sB),x) =
( AxB((SA,sB),x) =
( A(sA,x), A(sA,x), B(sB,x)); B(sB,x));
б) ( sA sA SA)
( SA)
( sB sB SB)
( SB)
( x x X) X)
 AxB((sA,sB),x) =
( AxB((sA,sB),x) =
( A(sA,x), A(sA,x), B(sB,x)); B(sB,x));
|
Иными словами, конечный автомат, являющийся прямым произведением двух конечных
автоматов, в качестве своих состояний имеет пары состояний исходных автоматов,
его начальное состояние есть пара их начальных состояний, выходной алфавит -
множество пар выходных символов автоматов-множителей, функции переходов и
выходов определены покомпонентно. Таким образом, прямое произведение конечных
автоматов - это просто два стоящих рядом невзаимодействующих конечных автомата,
синхронно работающих на одном общем ходе (рис. 6).
| Теорема 1. (Теорема Мура) |
Два конечных автомата А = <SA, X, YA, S0A,  A, A,  A.А> и В = <SB, X, YB, S0B, A.А> и В = <SB, X, YB, S0B,  B, B,  B> с одинаковым входным
алфавитом являются эквивалентами тогда и только тогда, когда для любого достижимого
состояния (SA, SB) в их прямом произведении А х В справедливо:
( B> с одинаковым входным
алфавитом являются эквивалентами тогда и только тогда, когда для любого достижимого
состояния (SA, SB) в их прямом произведении А х В справедливо:
( x x  Х) Х)  А (SA, х) = А (SA, х) =  В (SB, x). В (SB, x).
|
Доказательство.(Необходимость.) Пусть А и В эквивалентны, то есть
(

 X*)
X*)
 А *(S0A,
А *(S0A,
 ) =
) =
 В *(S0B,
В *(S0B,
 ).
).
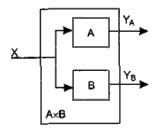
Рис. 6.
Прямое произведение конечных автоматов А и В
Докажем при этом предположении:
( (SA, SB)
(SA, SB) SA x SB) Достижимо
(SA, SB)
SA x SB) Достижимо
(SA, SB)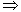 (
( x
x
 X)
X) A
(SA,X) =
A
(SA,X) =  B(SB, x).
B(SB, x).
В соответствии с определением 4, свойство достижимости состояния
(SA, SB) эквивалентно условию
(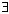

 X*)
X*) *((s0A, s0B)
*((s0A, s0B) ) = (sA,sB). Таким образом, надо доказать, что если
) = (sA,sB). Таким образом, надо доказать, что если
(

 X*)
X*)
 А *(S0B,
А *(S0B,
 ) =
) =
 В *(S0B,
В *(S0B,
 ), то
), то
( (sA,sB)
(sA,sB)
 SA
x SB)[(
SA
x SB)[(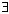
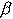
 X*)
X*)  *((s0A,s0B),
*((s0A,s0B), 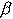 ) =
(sA,sB)
) =
(sA,sB) 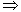 (
( x
x  X)
X) A(sA, x) =
A(sA, x) =
 B(sB, x)].
B(sB, x)].
Предположим противное, то есть что
 (
( (sA,sB)
(sA,sB)
 SA x SB)
[(
SA x SB)
[(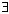
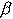
 X*)
X*)  *((s0A,s0B),
*((s0A,s0B), 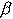 ) =
(sA,sB)
) =
(sA,sB) 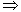 (
( x
x  X)
X) A(sA, x) =
A(sA, x) =
 B(sB, x)].
B(sB, x)].
и покажем, что тогда
 (
(

 X*)
X*)
 А *(S0A,
А *(S0A,
 ) =
) =  В *(S0B,
В *(S0B,  )
)
Отрицание следствия можно преобразовать в
(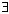 (sA,sB)
(sA,sB)
 SA x SB)[(
SA x SB)[(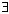
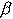
 X*)
X*)  *((s0A,s0B),
*((s0A,s0B), 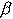 ) =
(sA,sB) & (
) =
(sA,sB) & (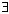 x
x  X)
X) A(sA, x)
A(sA, x) 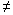
 B(sB, x)].
B(sB, x)].
Положим а = 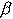 х. Очевидно, что:
х. Очевидно, что:
 A*(S0A,
A*(S0A,  ) =
) =
 A*(S0A,
A*(S0A,
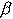 x) =
x) =
 A*(S0A,
A*(S0A,
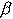 )
^
)
^ A(
A( *(S0A,
*(S0A,
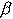 ), X) =
), X) =
 A*(S0A,
A*(S0A, 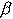 ) ^
) ^ A(
(SA, X)
A(
(SA, X) 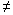
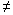
 B*(S0B,
B*(S0B, 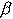 ) ^
) ^
 B(SB, x) =
B(SB, x) =  B*(S0B,
B*(S0B, 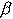 ) ^
) ^ B(
B( *(S0B,
*(S0B, 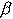 ), X) =
), X) =
 B*(S0B,
B*(S0B, 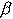 X) =
X) =  B* (SB,
B* (SB,  )
)
Отсюда:
(

 X*)
X*)
 A*(S0A,
A*(S0A,  ) или
) или
 (
(

 X*)
X*) A*(S0A,
A*(S0A,  ) =
) =  B*(S0B,
B*(S0B,  ),
),
что и требовалось доказать.
(Достаточность.) Докажем обратное, то есть в предположении
( (SA, sB)
(SA, sB)
 SAxSB)
SAxSB)
Достижимо
(SA, SB)  (
( x
x  Х)
Х)  А (SA, x) =
А (SA, x) =  B (SB, x)
B (SB, x)
докажем, что А и В эквивалентны, то есть
( x
x  Х*)
Х*)
 А* (S0A,
А* (S0A,
 ) =
) =  B
(S0B,
B
(S0B,  )
)
Это доказывается индукцией по длине входных цепочек. Иными словами, будем
доказывать
( k
k  Х)
(
Х)
(

 Хk)
Хk)  A*(S0A,
A*(S0A,
 ) =
) =
 B*(S0B,
B*(S0B,  )
для k = 0, 1, ...
)
для k = 0, 1, ...
Базой индукции является доказательство этого утверждения при k = 0.
Оно доказывается непосредственно подстановкой k = 0, поскольку
 A*(S0A, ε) =
A*(S0A, ε) =
 B*(S0B, ε) = ε при
входной цепочке е длиной 0.
B*(S0B, ε) = ε при
входной цепочке е длиной 0.
Шаг индукции. Пусть для некоторого i выполняется
(

 Xi)
Xi)
 A*(s0A,
A*(s0A,  ) =
) =
 B*(s0B,
B*(s0B,  ).
).
Докажем, что это выполнится и для i+1. Пусть  -
произвольная цепочка длиной i. Поскольку состояние
-
произвольная цепочка длиной i. Поскольку состояние
 A*(S0A,
A*(S0A,  )
в автомате А и состояние
)
в автомате А и состояние  B*(S0B,
B*(S0B,
 )
в автомате В являются достижимыми, из предположения
)
в автомате В являются достижимыми, из предположения
( (SA, SB)
(SA, SB)  SA x SB) Достижимо
(SA, SB)
SA x SB) Достижимо
(SA, SB) (
( x
x
 X)
X) A
(SA,X) =
A
(SA,X) =
 B(SB, x).
B(SB, x).
следует:
( x
x  X)
X)
 A(
A( A*
(s0A,
A*
(s0A,  ) x ) =
) x ) =
 B(
B( B
*(s0B,
B
*(s0B,  ) x ).
) x ).
Отсюда: ( x
x  X)
(
X)
(

 Xi)
Xi)
 A *(s0A,
A *(s0A,
 x) =
x) =
 B*(s0B,
B*(s0B,
 x).
x).
Но при произвольном 
 Xi и произвольном x
Xi и произвольном x
 X очевидно,
что
X очевидно,
что  x -
произвольная цепочка из Xi+1.
x -
произвольная цепочка из Xi+1.
Теорема доказана.
Пример 2 (продолжение)
Прямое произведение конечных автоматов А и В, изображенных на рис. 5,
представлено на рис. 7, а. На рис. 7, б показан этот же автомат с выброшенными
недостижимыми состояниями. По графу переходов видно, что из всех достижимых
состояний под воздействием входных сигналов автомат А х В выдает пары
одинаковых выходных сигналов. Следовательно, автоматы А и В эквивалентны.
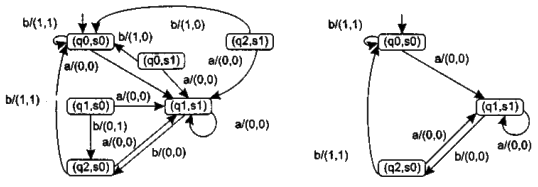
Рис. 7. Прямое произведение конечных
автоматов примера 2
[Список тем]
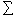 - алфавит (конечное множество
символов) и
- алфавит (конечное множество
символов) и 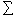 * множество
цепочек из элементов
* множество
цепочек из элементов 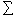 . Будем о
бозначать ε пустую цепочку, вовсе не содержащую символов, а ^ - операцию
конкатенации (склеивания) цепочек. Так, аав^ва = аавва. Знак операции
конкатенации часто опускают. Цепочки будем обозначать малыми греческими
буквами
. Будем о
бозначать ε пустую цепочку, вовсе не содержащую символов, а ^ - операцию
конкатенации (склеивания) цепочек. Так, аав^ва = аавва. Знак операции
конкатенации часто опускают. Цепочки будем обозначать малыми греческими
буквами
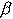 ,
,
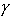 .
Очевидно, ε является как левой, так и правой единицей
для операции конкатенации:
аε = εа = а.
.
Очевидно, ε является как левой, так и правой единицей
для операции конкатенации:
аε = εа = а.
 ,
,
 > - конечный автомат.
> - конечный автомат.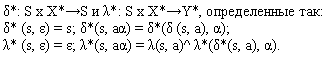
 S называется
достижимым тогда и только тогда, когда (
S называется
достижимым тогда и только тогда, когда ( 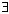

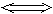 (
(
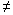 s.
s.

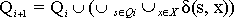 .
Очевидно также, что не более чем за |S| шагов
Qk+i = Qk.
Это множество состояний Qk будет включать в себя все
достижимые состояния автомата
А = <S, X, Y, s0,
.
Очевидно также, что не более чем за |S| шагов
Qk+i = Qk.
Это множество состояний Qk будет включать в себя все
достижимые состояния автомата
А = <S, X, Y, s0,
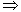 (
( (
(